Saturday brings a fresh set of NYT Pips puzzles. Today's set features a mix of exact number requirements and inequality conditions that will test your domino placement strategy. We've got hints, step-by-step walkthroughs, and full solutions for Easy, Medium, and Hard difficulty levels.
How to Play Pips
Pips is a domino placement puzzle where you fill a grid of color-coded zones. Each zone has a condition you must satisfy using the pip values on your dominoes. The twist: you must use every domino and meet every condition to win.
Zone Conditions:
- = All pips in this zone must equal the same number
- Not Equal All pips must be different numbers
- > Pips must be greater than the listed number
- < Pips must be less than the listed number
- Exact Number Pips must total that exact value
- No Color Free space, any domino value works
Click or tap dominoes to rotate them. Each puzzle has one or more valid solutions.
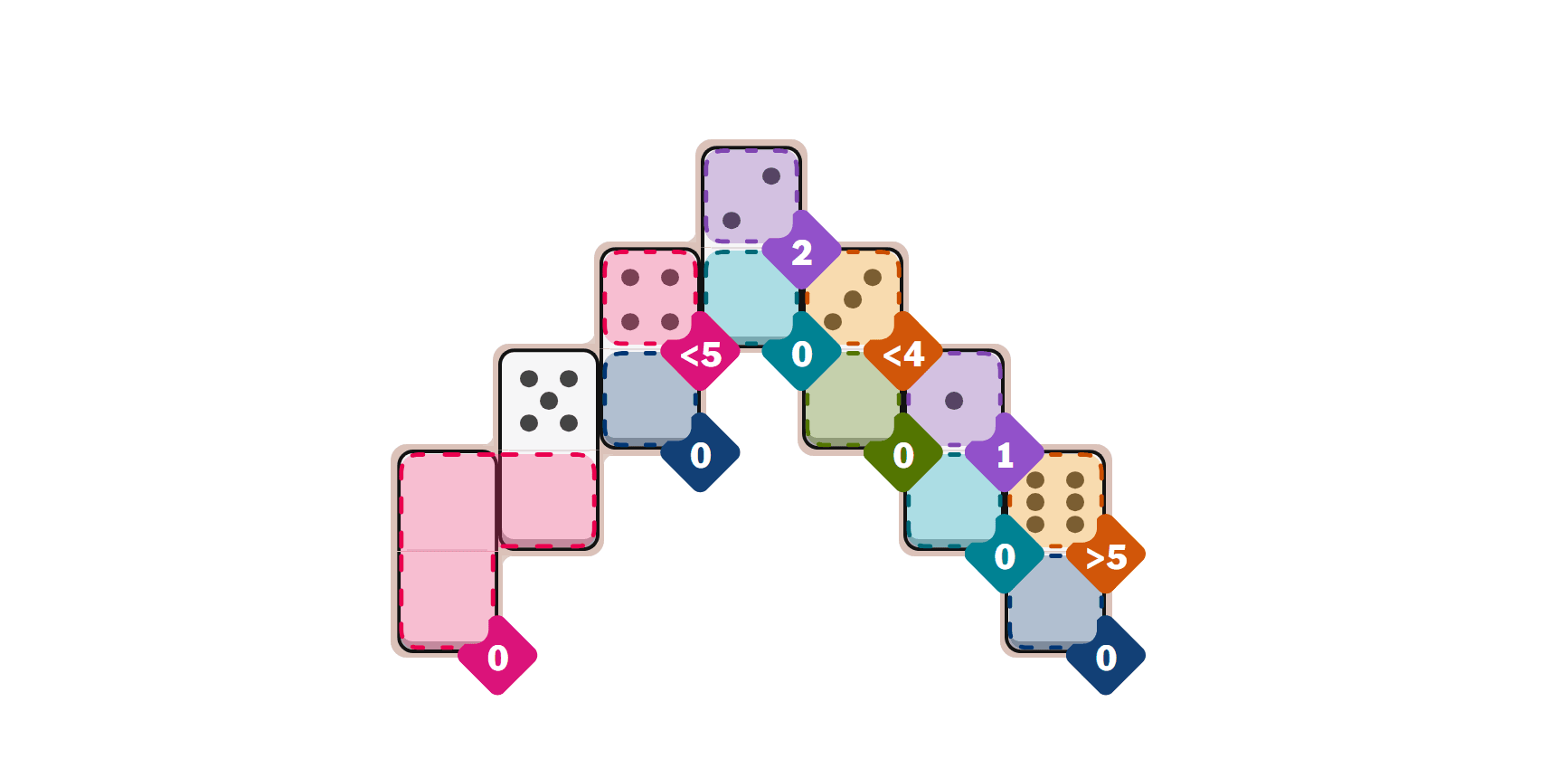
Today's Easy Pips
Quick Hints (No Spoilers)
Starting Point: Begin with the Number (0) zones - they require dominoes that sum to exactly zero, which means you'll need dominoes with zeros on both ends.
Key Insight: The dominoes with zeros on one side can bridge between the Number (0) zones and other zones with different requirements.
Step-by-Step Walkthrough
- 1.Start with the 0/0 domino - it must go in a Number (0) zone since both sides are zero.
- 2.Place the 5/0 domino vertically in another Number (0) zone, with the zero side touching the zone boundary.
- 3.The 4/0 domino goes vertically in both a Number (0) zone and the Less Than (5) zone - the 4 satisfies the less-than condition.
- 4.Place the 2/0 domino vertically in the Number (2) zone and a Number (0) zone - the 2 side gives you the exact total of 2.
- 5.The 3/0 domino fits vertically in the Less Than (4) zone and a Number (0) zone - 3 is less than 4.
- 6.Place the 1/0 domino vertically in the Number (1) zone and a Number (0) zone - the 1 side gives you the exact total of 1.
- 7.Finally, place the 6/0 domino vertically in the Greater Than (5) zone and a Number (0) zone - 6 is greater than 5.
Easy Pips Solution
Scroll past if you want to keep trying
---
---
---
---
- 1.Place the 0/0 domino vertically in the Number (0) zone
- 2.Place the 5/0 domino vertically in the Number (0) zone
- 3.Place the 4/0 domino vertically in the Number (0) zone and Less Than (5) zone
- 4.Place the 2/0 domino vertically in the Number (2) zone and Number (0) zone
- 5.Place the 3/0 domino vertically in the Less Than (4) zone and Number (0) zone
- 6.Place the 1/0 domino vertically in the Number (1) zone and Number (0) zone
- 7.Place the 6/0 domino vertically in the Greater Than (5) zone and Number (0) zone
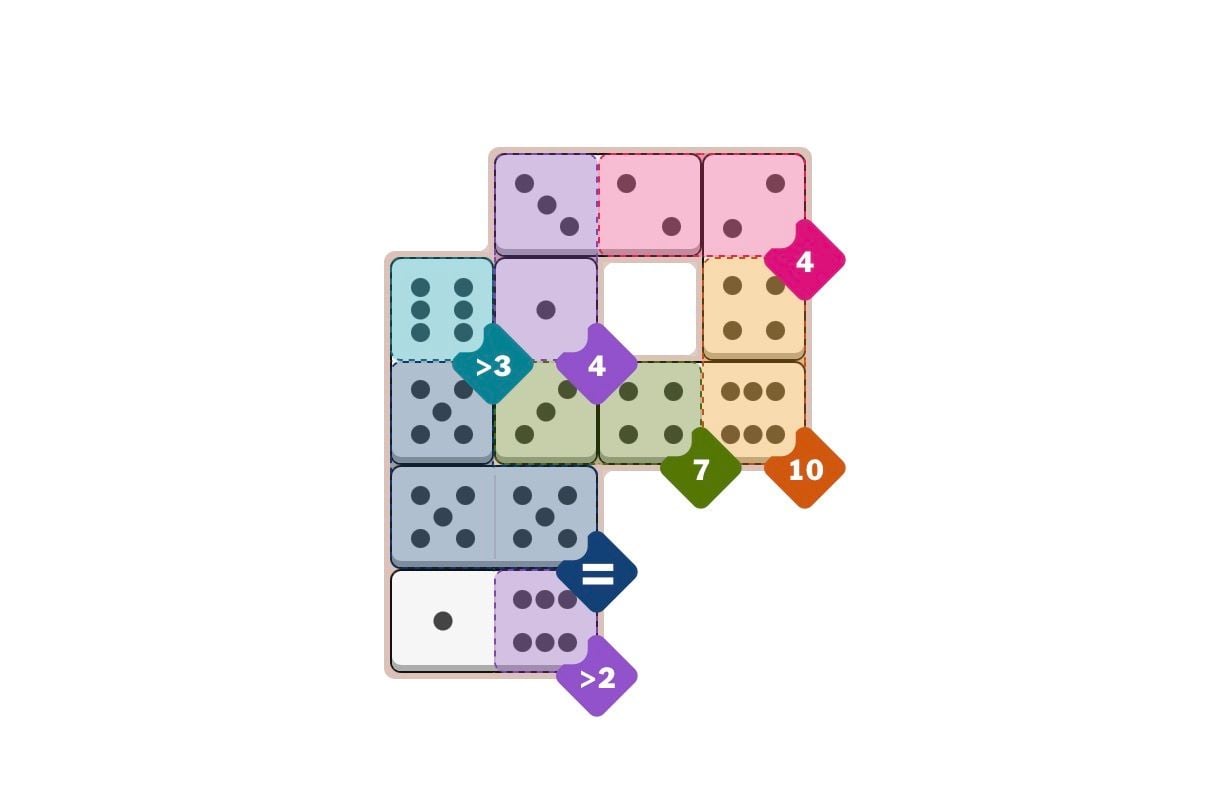
Today's Medium Pips
Quick Hints (No Spoilers)
Starting Point: Look at the Equal (5) zone first - you need dominoes where both ends equal 5, which means the 5/5 domino is your only option.
Key Insight: The 6/5 domino is critical for connecting the Greater Than (3) zone with the Equal (5) zone - the 6 side satisfies greater than 3, while the 5 side works in the equal zone.
Step-by-Step Walkthrough
- 1.Place the 5/5 domino horizontally in the Equal (5) zone - this is the only domino that can satisfy the "all pips must equal 5" condition.
- 2.Place the 6/5 domino vertically so the 6 side is in the Greater Than (3) zone and the 5 side is in the Equal (5) zone.
- 3.The 1/3 domino goes vertically with the 1 side in a Number (4) zone and the 3 side in the Number (7) zone.
- 4.Place the 3/2 domino horizontally across two Number (4) zones - the 3+2 gives you the exact total of 5, but since it's split across two zones, each zone gets either 3 or 2.
- 5.The 2/4 domino fits vertically with the 2 side in a Number (4) zone and the 4 side in the Number (10) zone.
- 6.Place the 4/6 domino horizontally with the 4 side in the Number (7) zone and the 6 side in the Number (10) zone.
- 7.Finally, place the 1/6 domino horizontally in the Greater Than (2) zone - both 1 and 6 are greater than 2.
Medium Pips Solution
Scroll past if you want to keep trying
---
---
---
---
- 1.Place the 6/5 domino vertically in the Greater Than (3) zone and Equal (5) zone
- 2.Place the 1/3 domino vertically in the Number (4) zone and Number (7) zone
- 3.Place the 3/2 domino horizontally in the Number (4) zone (two zones)
- 4.Place the 2/4 domino vertically in the Number (4) zone and Number (10) zone
- 5.Place the 4/6 domino horizontally in the Number (7) zone and Number (10) zone
- 6.Place the 5/5 domino horizontally in the Equal (5) zone
- 7.Place the 1/6 domino horizontally in the Greater Than (2) zone
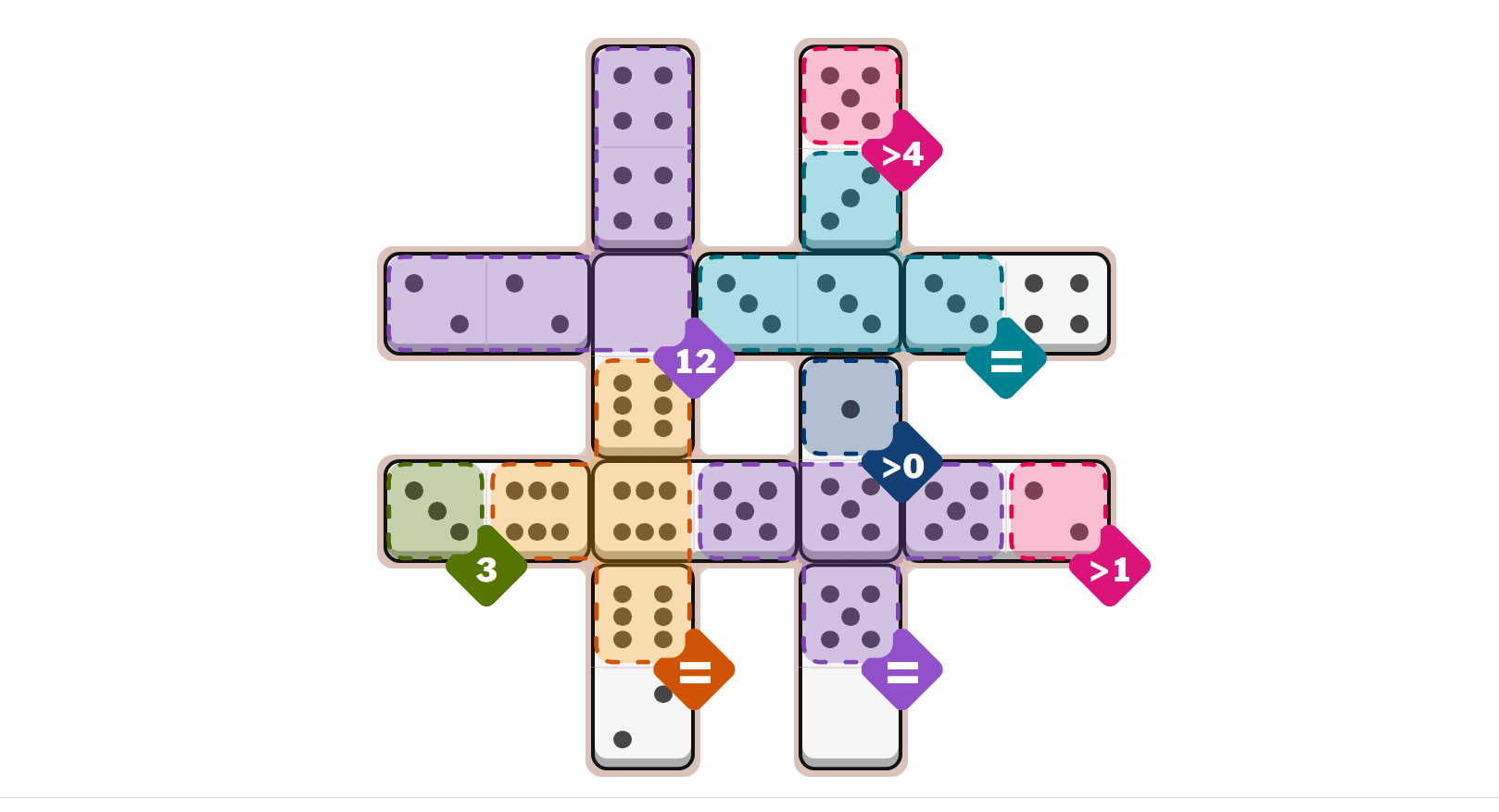
Today's Hard Pips
Quick Hints (No Spoilers)
Starting Point: Tackle the Number zones first - the Number (12) and Number (3) zones have exact total requirements that will dictate which dominoes must go there.
Key Insight: The Equal zones (3, 5, and 6) require dominoes where both ends match the specified number, but dominoes can bridge between equal zones and other zones.
Watch Out For: The dominoes that can satisfy multiple equal zones simultaneously - like the 6/5 domino that works in both Equal (6) and Equal (5) zones.
Step-by-Step Walkthrough
- 1.Start with the Number (12) zone - you need dominoes that sum to exactly 12. Place the 4/4 domino vertically (4+4=8) and the 2/2 domino horizontally (2+2=4) to reach 12 total.
- 2.The 0/6 domino goes vertically with the 0 side in the Number (12) zone (0 doesn't affect the total) and the 6 side in the Equal (6) zone.
- 3.Place the 3/6 domino horizontally with the 3 side in the Number (3) zone and the 6 side in the Equal (6) zone - this gives you the exact total of 3 for that zone.
- 4.Now address the Equal (6) zone - place the 6/5 domino horizontally with the 6 side in Equal (6) zone and the 5 side in Equal (5) zone.
- 5.Place the 6/2 domino vertically in the Equal (6) zone - the 6 side satisfies the equal condition.
- 6.The 5/3 domino goes vertically with the 5 side in the Greater Than (4) zone and the 3 side in the Equal (3) zone.
- 7.Place the 3/3 domino horizontally in the Equal (3) zone - both sides equal 3.
- 8.The 3/4 domino fits horizontally in the Equal (3) zone - the 3 side satisfies the equal condition.
- 9.Place the 5/0 domino vertically in the Equal (5) zone - the 5 side satisfies the equal condition.
- 10.Finally, place the 1/5 domino vertically with the 1 side in the Greater Than (0) zone and the 5 side in the Equal (5) zone.
- 11.Complete the puzzle with the 5/2 domino horizontally in the Greater Than (1) zone and Equal (5) zone.
Hard Pips Solution
Last chance to solve independently
---
---
---
---
- 1.Place the 4/4 domino vertically in the Number (12) zone
- 2.Place the 2/2 domino horizontally in the Number (12) zone
- 3.Place the 0/6 domino vertically in the Number (12) zone and Equal (6) zone
- 4.Place the 3/6 domino horizontally in the Number (3) zone and Equal (6) zone
- 5.Place the 6/5 domino horizontally in the Equal (6) zone and Equal (5) zone
- 6.Place the 6/2 domino vertically in the Equal (6) zone
- 7.Place the 5/3 domino vertically in the Greater Than (4) zone and Equal (3) zone
- 8.Place the 3/3 domino horizontally in the Equal (3) zone
- 9.Place the 3/4 domino horizontally in the Equal (3) zone
- 10.Place the 5/0 domino vertically in the Equal (5) zone
- 11.Place the 1/5 domino vertically in the Greater Than (0) zone and Equal (5) zone
- 12.Place the 5/2 domino horizontally in the Greater Than (1) zone and Equal (5) zone
Puzzle Debrief
Overall Difficulty: Moderate challenge with a clear progression from straightforward number matching to complex zone bridging.
Trickiest Puzzle: Hard - the multiple equal zones (3, 5, and 6) create constraints that dominoes must satisfy simultaneously, requiring careful planning of which dominoes bridge between zones.
Our Take: Today's puzzles effectively teach domino placement strategy through zone constraints. The progression from simple exact totals to multiple equal zones demonstrates how dominoes can serve dual purposes when placed on zone boundaries. The Hard puzzle's requirement to satisfy three different equal conditions simultaneously is particularly instructive for advanced play.
Tomorrow's Pips drops at midnight. See you then.















